Review of Probability and Statistics
January 16, 2025
Preview of next 6 lectures
Upcoming lecture series
Lecture 4: Review of Probability and Statistics
Lecture 5: Statistical Inference - two group comparisons
Lecture 6: Statistical Inference - linear regression and ANOVA
Lecture 7: Statistical Inference - multiple linear regression
Lecture 8: Statistical Inference - continuous regression + limma
Lecture 9: Statistical Inference - multiple testing
What is Statistics?
- The field of statistics concerns the science of collecting, analyzing/modeling, interpreting data and communicating uncertainty about the results
- Statistics is not a collection of generic “recipes” to follow
- Data science and machine learning have facilitated application to ‘big data’
Our (statistical) goals for this course:
gain a rigorous understanding of core principles of common analyses of high-dimensional biological data
build solid foundation to follow up on specific topics
Today: review terminology and basic concepts
- The relationship between statistical inference and probability
- Random variables and their probability distributions
- Models, parameters, and their estimators
- Central Limit Theorem (CLT)
- Hypothesis testing
Learning objectives:
Be familiar with the terminology: describe data as random variables with various types of sampling distributions
Gain intuition for the central concepts: understand how statistical inference and modeling can help us learn about the properties of a population
Statistical Inference
A framework for generating conclusions about a population from a sample of noisy data
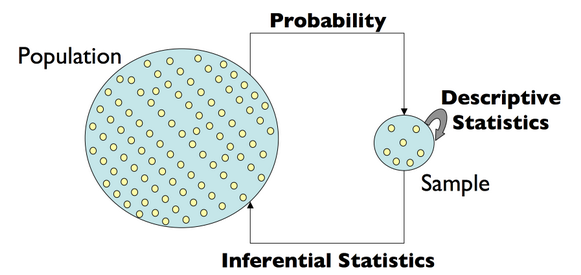
- Language of probability enables us to discuss uncertainty and make predictions
- Statistical inference enables us to make conclusions about the data
- We need both to learn from data
Variables
Definition
Variable: an element, feature, or factor that is liable to vary or change
In statistical terminology, a variable is an unknown quantity that we’d like to study
Most research questions can be formulated as: “What’s the relationship between two or more variables?”
Random variables
Definition
Random Variable (RV): A variable whose value results from the measurement of a quantity that is subject to variation (e.g. the outcome an experiment)
Examples: a coin flip, a dice throw, the expression level of gene X
An RV has a probability distribution
Distributions of Random Variables (RVs)
Definition
Probability: A number assigned to an outcome/event that describes the extent to which it is likely to occur
Probability must satisfy certain rules (e.g. be between 0 and 1)
Probability represents the (long-term) frequency of an event
Definition
Probability distribution: A mathematical function that maps outcomes/events to probabilities
Example experiment: Two coin tosses
Experiment: Toss two coins
Sample space: set of all possible outcomes \(S=\{TT, HT, TH, HH\}\)
Random Variable of interest: number of heads
| Outcome | Number of Heads |
|---|
Example experiment: Two coin tosses
Experiment: Toss two coins
Sample space: set of all possible outcomes \(S=\{TT, HT, TH, HH\}\)
Random Variable of interest: number of heads
| Outcome | Number of Heads | |
|---|---|---|
| TT |   |
0 |
| HT |   |
1 |
| TH |   |
1 |
| HH |   |
2 |
Assigning probability to outcomes
Let:
\(\omega=\) an outcome
\(X(\omega)=\) number of heads in \(\omega\) (RV)
Each possible outcome is associated with a probability
Event: A set of outcomes that satisfy some condition
Each realization of the RV corresponds to an event (e.g. \(X(\omega)=1\) corresponds to the outcomes \(TH\) and \(HT\) )
| \(\omega\) | \(X(\omega)\) | Probability | |
|---|---|---|---|
| TT |   |
0 | |
| HT |   |
1 | |
| TH |   |
1 | |
| HH |   |
2 |
Assigning probability to events
The probability distribution of the Random Variable \(X\) tells us how likely each event (number of heads) is to occur in the experiment
| Event | \(x\) | \(P(X=x)\) |
|---|---|---|
  |
||
  , ,   |
||
  |
Note on notation: \(P(X=x)\) can also be written as \(P_X(x)\)
Two types of random variables
A discrete RV has a countable number of possible values
- e.g. coin flip, throwing dice, genotype at a particular locus
A continuous RV takes on values in an interval of numbers
- e.g. blood glucose level, height of individuals
Discrete or Continuous?
survival time
number of chromosomes
mRNA expression level
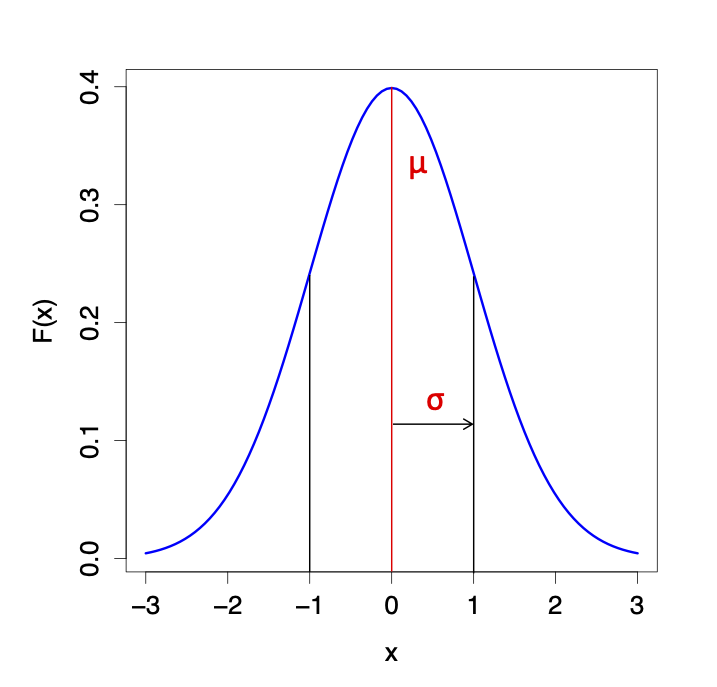
Standard Gaussian (Normal) distribution
probability density function (pdf): \[f(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]
Parameters: quantities that summarize a population
- Mean \(=\mu\)
- Standard Deviation \(=\sigma\)
For convenience, we write \(N(\mu, \sigma^2)\)
When \(\mu=0\) and \(\sigma=1\), this is the Standard Normal distribution \(N(0,1)\)
Gaussian (Normal) distribution

\[\text{pdf: }f(x|\mu,\sigma^2) = \phi(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]
Density \(\rightarrow\) probability requires integration
In coin flip example, we could sum up discrete probabilities - not the case for continuous RVs
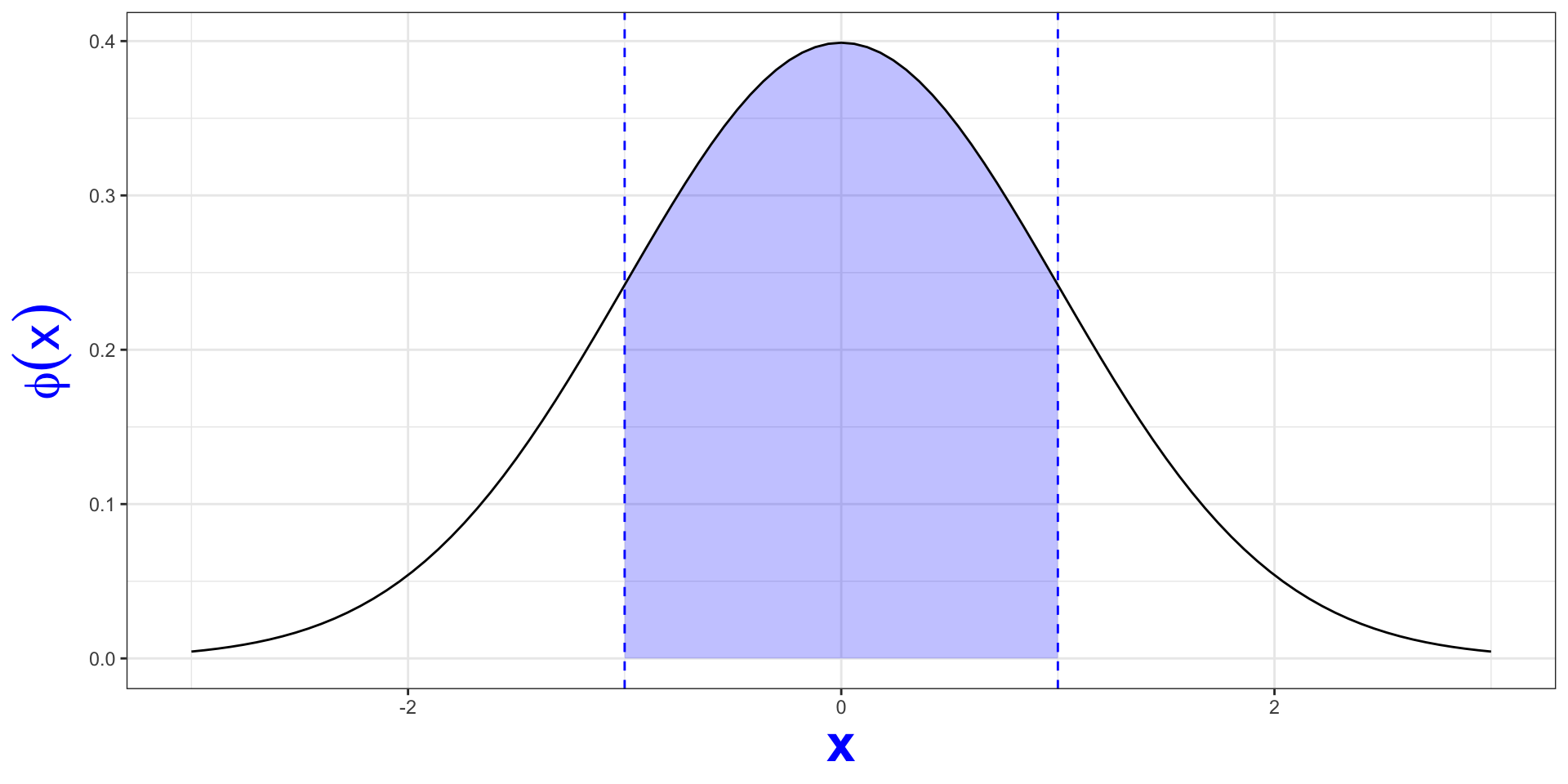
Empirical Rule for Normal Distributions

Statistical Inference
The parameter space is the set of all possible values of a parameter
One major goal: to “figure out” (i.e. estimate) the parameter values
- i.e. fit the model to the data
Note
A model is a representation that (we hope) approximates the data and (more importantly) the population that the data were sampled from
- We can then use this model for:
- hypothesis testing
- prediction
- simulation
Statistical Inference

IID
- A requirement (assumption) in many settings is that the data are IID: Independent and Identically Distributed
- Identically Distributed: a set of observations (events) are from the same population
- i.e. they have the same underlying probability distribution
- e.g. a t-test assumes that under the null, all observations come from the same normal distribution
- Independent: Events \(A\) and \(B\) are independent if and only if \(P(A,B) = P(A)P(B)\)
- i.e. the joint probability is the product of the individual event probabilities
- The above statement is for two events, but the same definition applies for any number of events
Violations of independence
Caution
If our analysis relies on the assumption that our observations are independent and they are not, our conclusions might be misleading
Experimental design is in part about trying to avoid unwanted dependence
Example of a design with unwanted dependence:
- Height measurements of individuals sampled from related females in a particular family are not independent
Recall: parameters of the normal distribution

\[f(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]
Mean \(=\mu\)
Standard Deviation \(=\sigma\)
For convenience, we write \(N(\mu, \sigma^2)\)
Population parameters are unknown1 (underlying properties of the population)
Parameter estimation
Estimator: A function (or rule) used to estimate a parameter of interest
Estimate: A particular realization (value) of an estimator
Estimators for normally distributed data
If we are given a sample of \(n\) observations from a normally distributed population, how do we estimate the parameter values \(\mu\) and \(\sigma\)?
Recall \(\mu\) is the mean and \(\sigma\) the standard deviation of the distribution
\[\hat{\mu} = \bar{x} = \frac{x_1 + x_2 + ... + x_n}{n} = \frac{1}{n} \sum_{i=1}^n x_i\]
\[\hat{\sigma} = s = \sqrt{\frac{\sum_{i=1}^n(x_i - \bar{x})^2}{n-1}}\]
Estimators vs Parameters
| Estimators | Parameters | |
|---|---|---|
| Summarize | Sample | Population (ground truth) |
| Value | Computed from data | Unknown |
| Notation | \(\hat{\theta}\) | \(\theta\) |
Normal Mean: Estimator vs Parameter
| Estimator | Parameter | |
|---|---|---|
| Summarizes | Sample/data | Population (ground truth) |
| Value | \(\bar{x}=\frac{1}{n} \sum_{i=1}^n x_i\) | Unknown |
| Notation | \(\hat{\mu}\) | \(\mu\) |
Normal Standard Deviation: Estimator vs Parameter
| Estimator | Parameter | |
|---|---|---|
| Summarizes | Sample/data | Population (ground truth) |
| Value | \(s=\sqrt{\frac{\sum_{i=1}^n(x_i - \bar{x})^2}{n-1}}\) | Unknown |
| Notation | \(\hat{\sigma}\) | \(\sigma\) |
Estimator for normally distributed data
Let’s say we collected a sample from a population we assume to be normal
We estimate the mean \(\large \hat{\mu}=\bar{x}\)
How good is the estimate?
Sampling distribution
Statistic: any quantity computed from values in a sample
Any function (or statistic) of a sample (data) is a random variable
Thus, any statistic (because it is random) has its own probability distribution function \(\rightarrow\) specifically, we call this the sampling distribution
Example: the sampling distribution of the mean
Sampling distribution of the mean
The sample mean \(\large \bar{x}\) is a RV, so it has a probability or sampling distribution
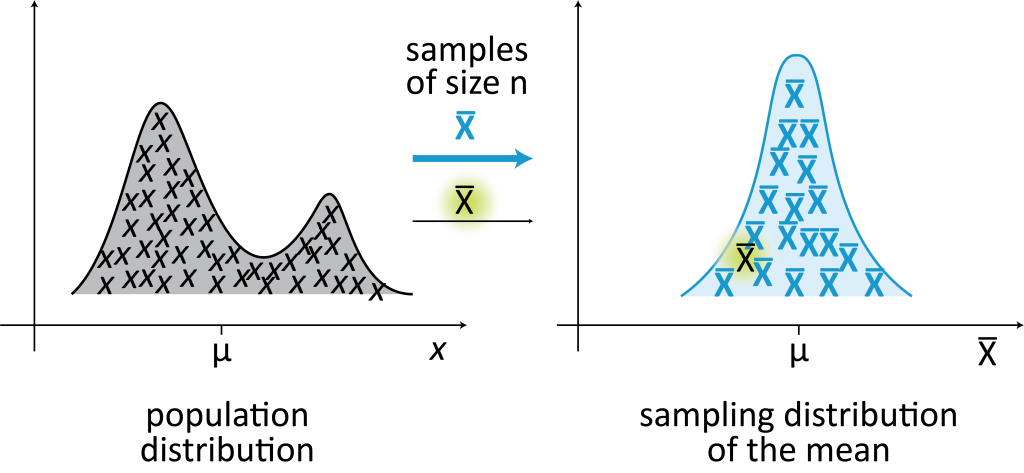
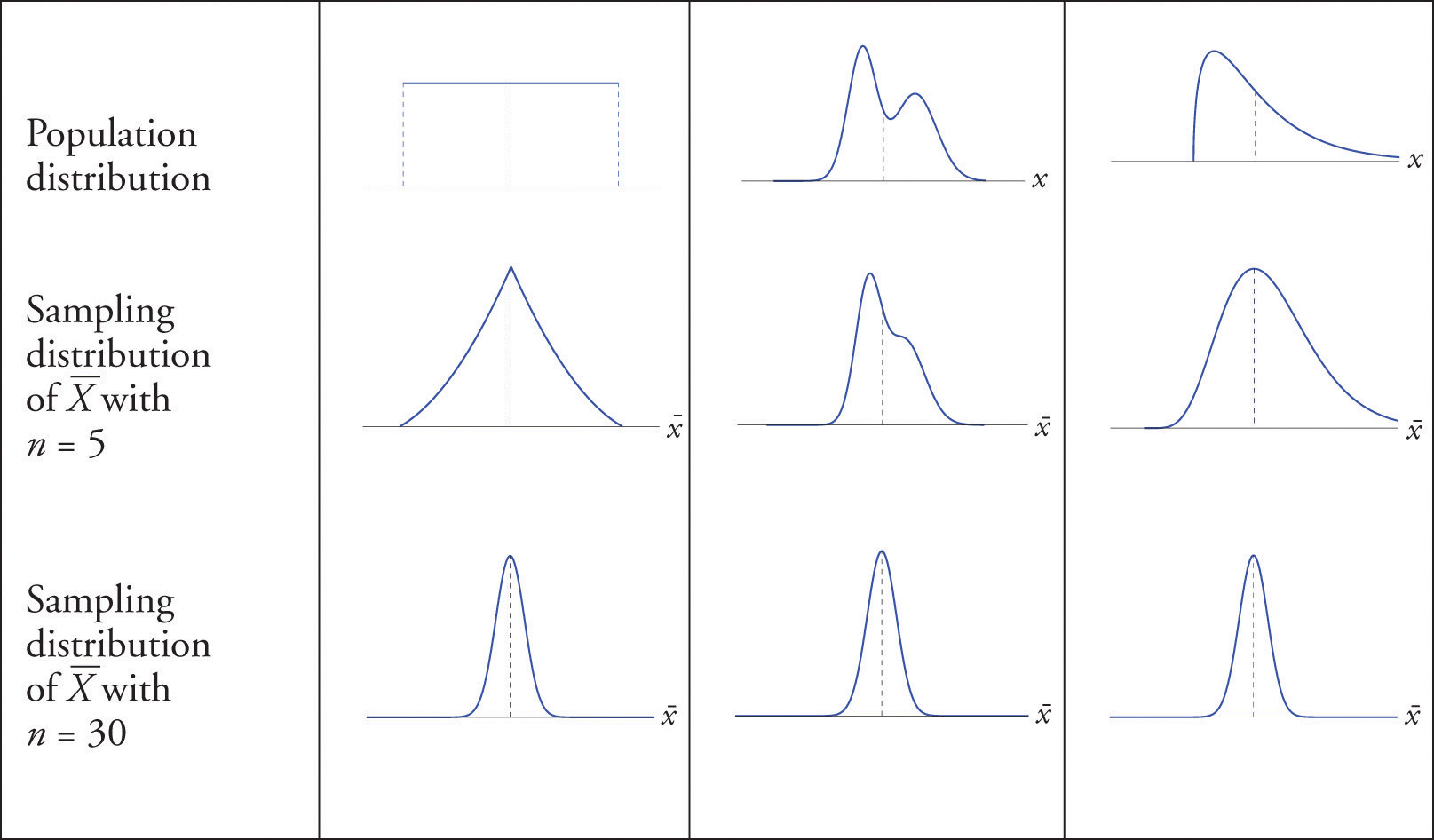
Central Limit Theorem (CLT)
By the Central Limit Theorem (CLT), we know that the sampling distribution of the mean (of \(n\) observations) is Normal with mean \(\mu_{\bar{X}} = \mu\) and standard deviation \(\sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}}\)
Standard deviation vs standard error
Warning
The standard deviation is not the same as the standard error
Standard error describes variability across multiple samples in a population
Standard deviation describes variability within a single sample
The sampling distribution of the mean of \(n\) observations (by CLT): \[\bar{X} \sim N(\mu, \frac{\sigma^2}{n})\]
The standard error of the mean is \(\frac{\sigma}{\sqrt{n}}\)
The standard deviation of \(X\) is \(\sigma\)
Estimation of parameters of the sampling distribution of the mean
Just as we estimated \(\mu\) and \(\sigma\) for our sample of \(n\) observations from a normally distributed population before, we can also estimate \(\mu_{\bar{X}}\) and \(\sigma_{\bar{X}}\):
\(\hat{\mu}_{\bar{X}} = \hat{\mu} = \bar{x}\)
\(\hat{\sigma}_{\bar{X}} = \frac{\hat{\sigma}}{\sqrt{n}} = \frac{s}{\sqrt{n}}\)
Standard error of the mean
\[\large\hat{\sigma}_{\bar{X}} = \frac{\hat{\sigma}}{\sqrt{n}} = \frac{s}{\sqrt{n}}\]
The standard error (SE) of the mean reflects uncertainty about our estimate of the population mean \(\large\hat{\mu}\)
For the distributional assumptions to hold, the CLT assumes a ‘large enough’ sample:
Rule of thumb: when the sample size is ~30 or more, the normal distribution is a good approximation for the sampling distribution of the mean
for smaller samples, the SE \(\large\frac{s}{\sqrt{n}}\) is an underestimate
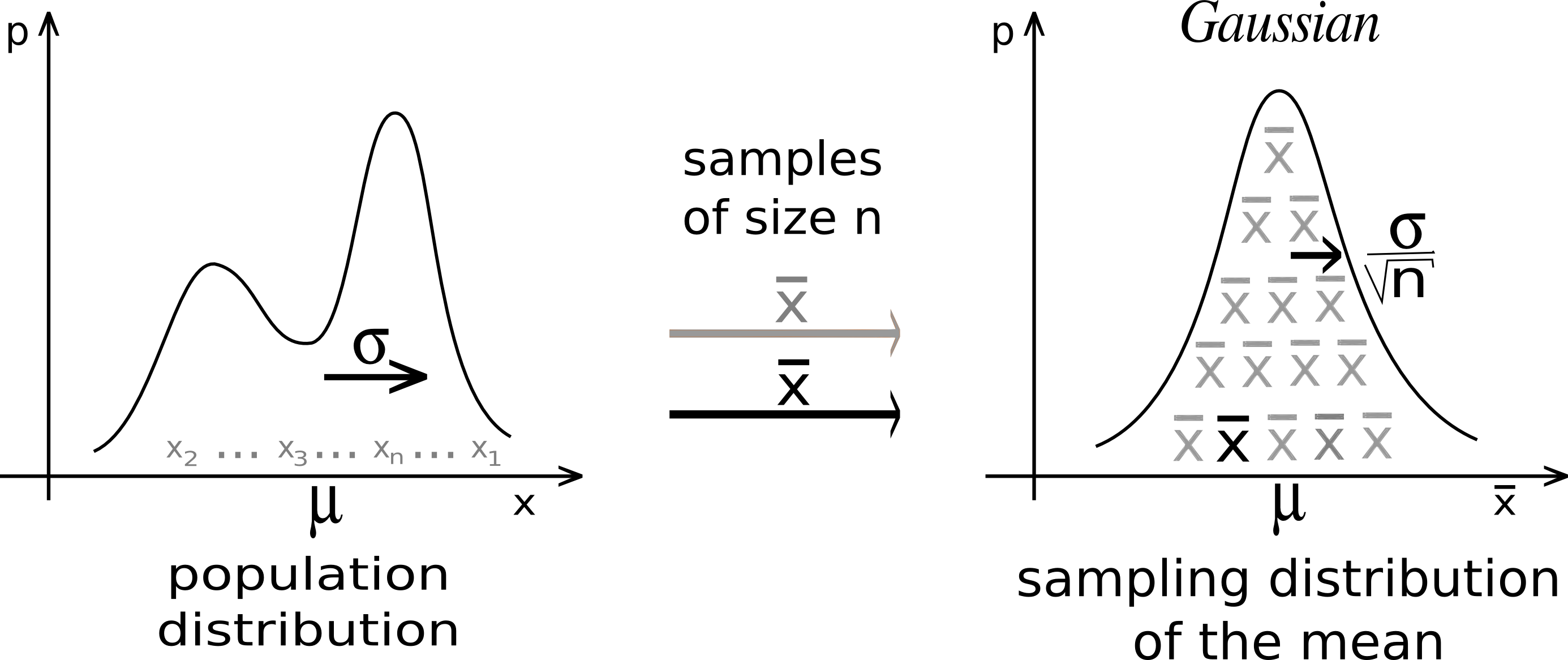
CLT applies to any population…
…regardless of distribution
Let \(\normalsize X_1, X_2, ..., X_n\) be a random sample from a population with a non-normal distribution
If the sample size \(\normalsize n\) is sufficiently large, then the sampling distribution of the mean will be approximately normal: \(\normalsize \bar{X} \sim N(\mu, \frac{\sigma^2}{n})\)
Illustration (n = 3)
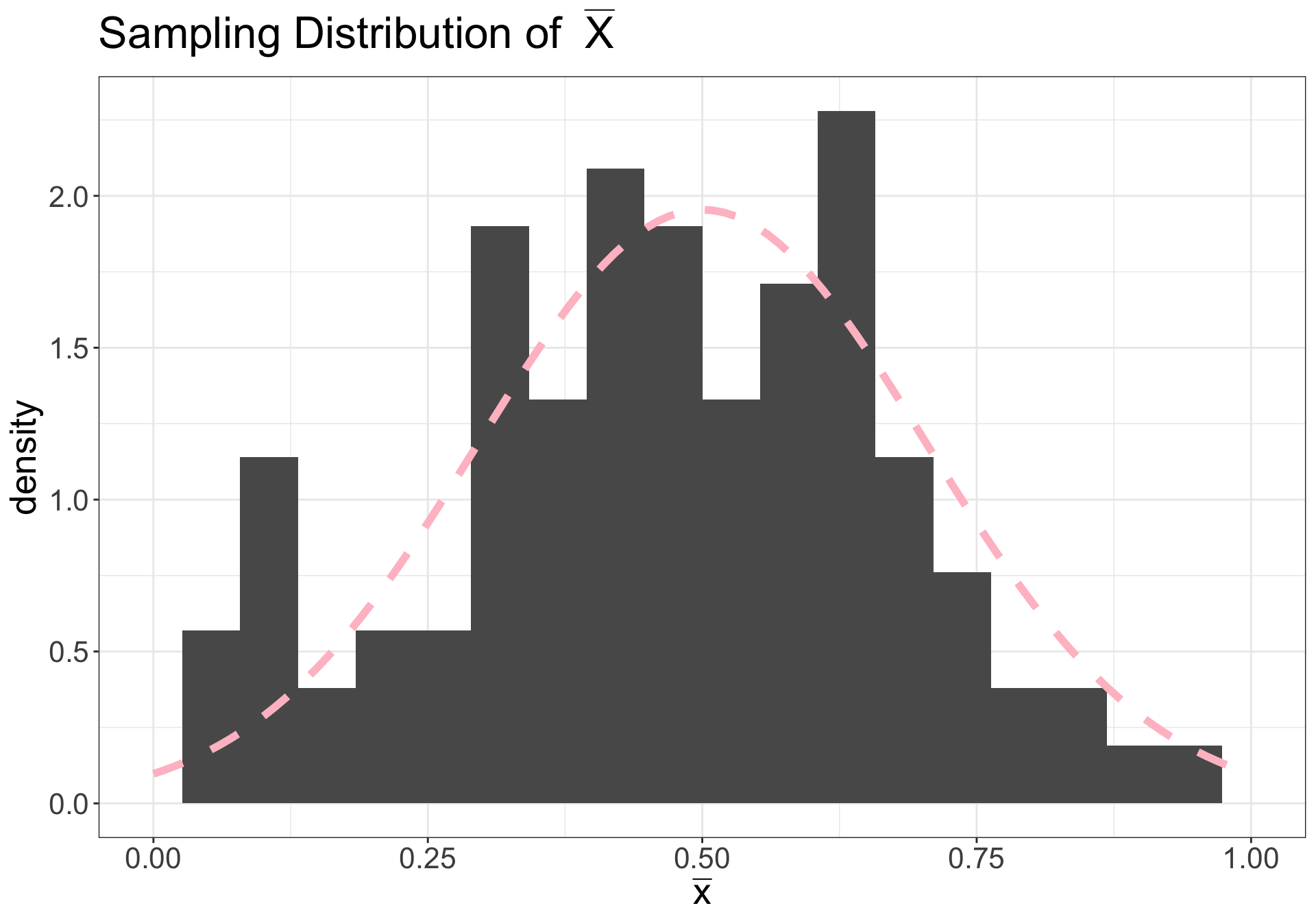
On right: dashed pink line is \(N(\mu, \sigma^2/n)\)
Illustration (n = 10)
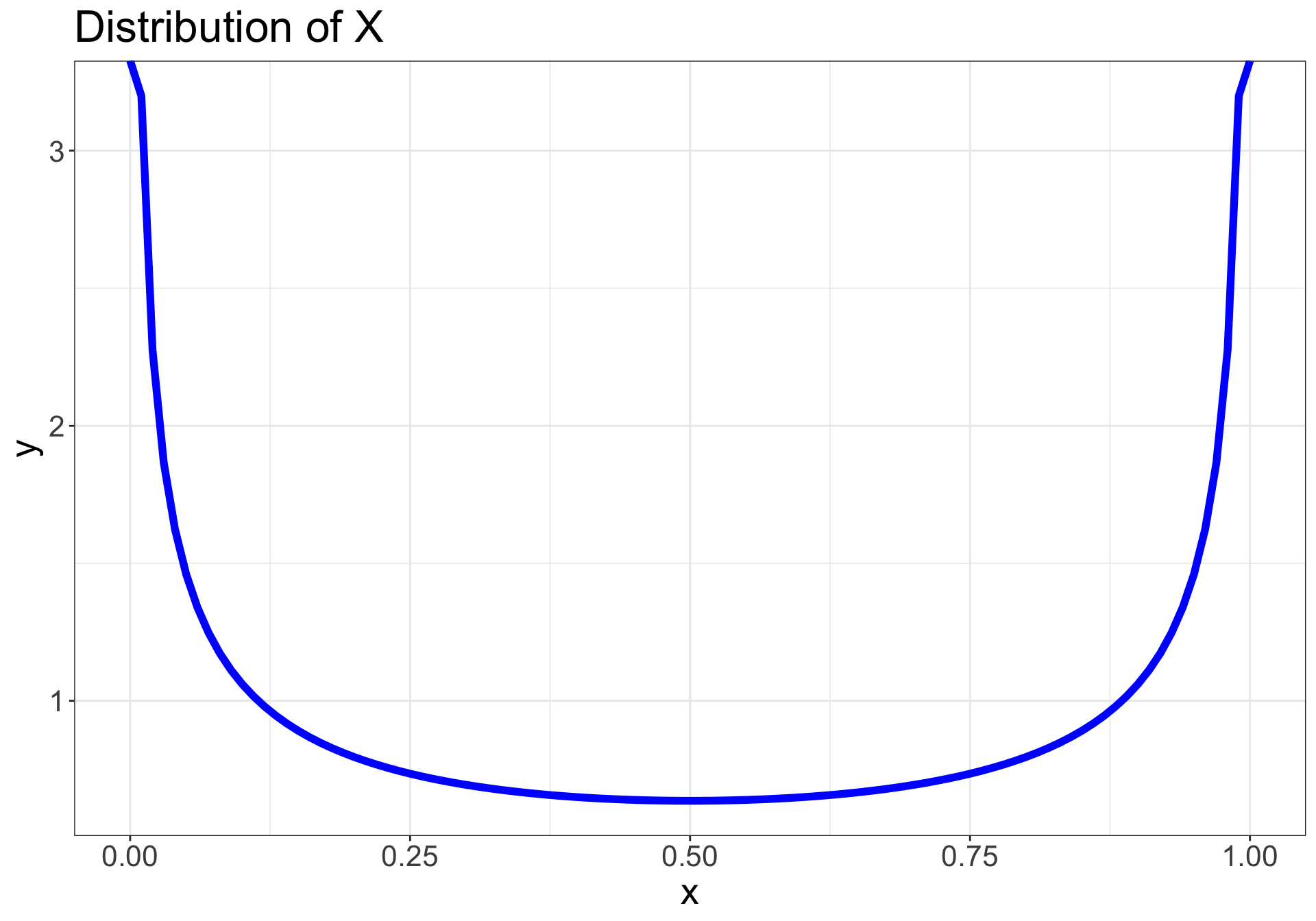
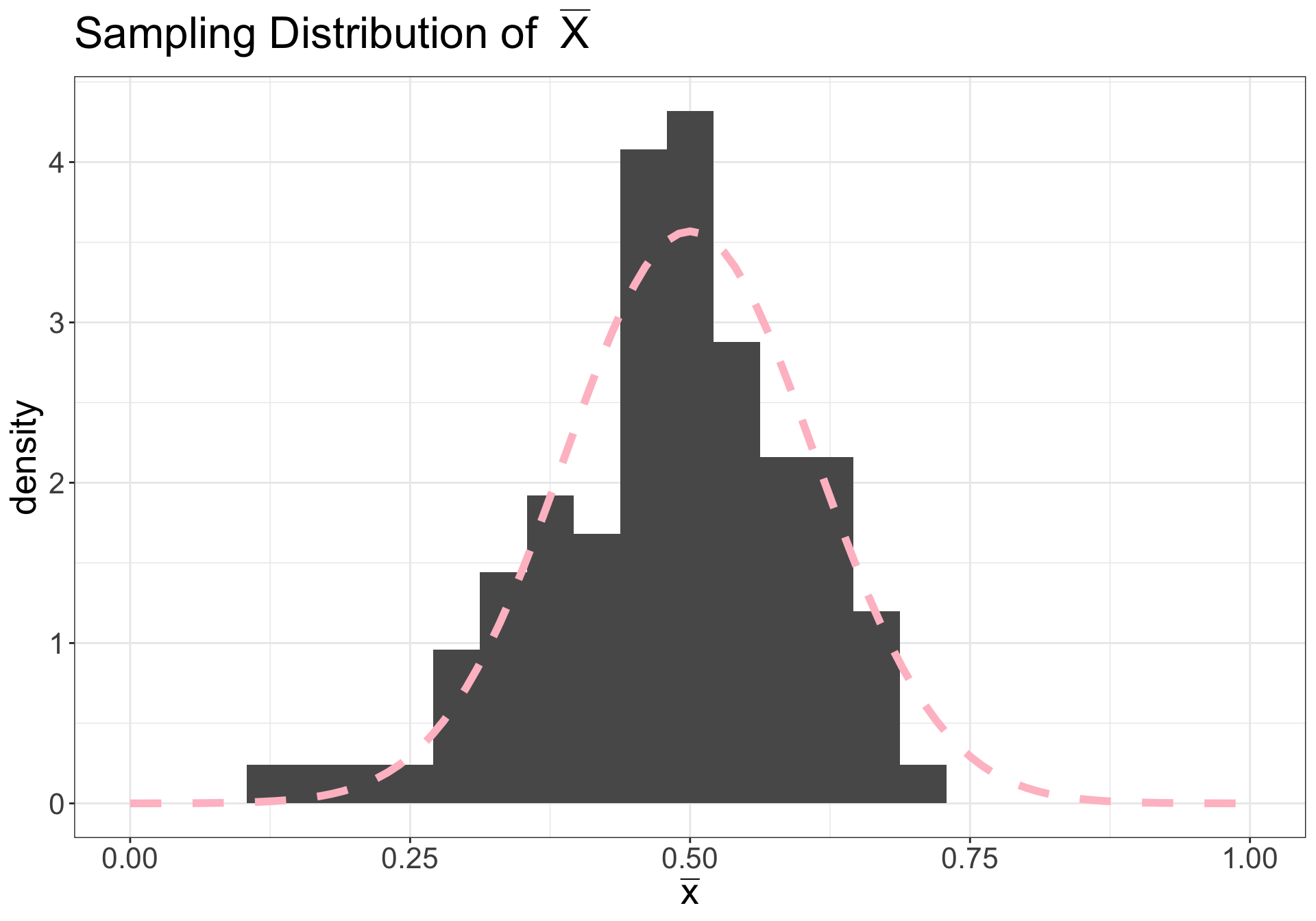
On right: dashed pink line is \(N(\mu, \sigma^2/n)\)
Illustration (n = 30)
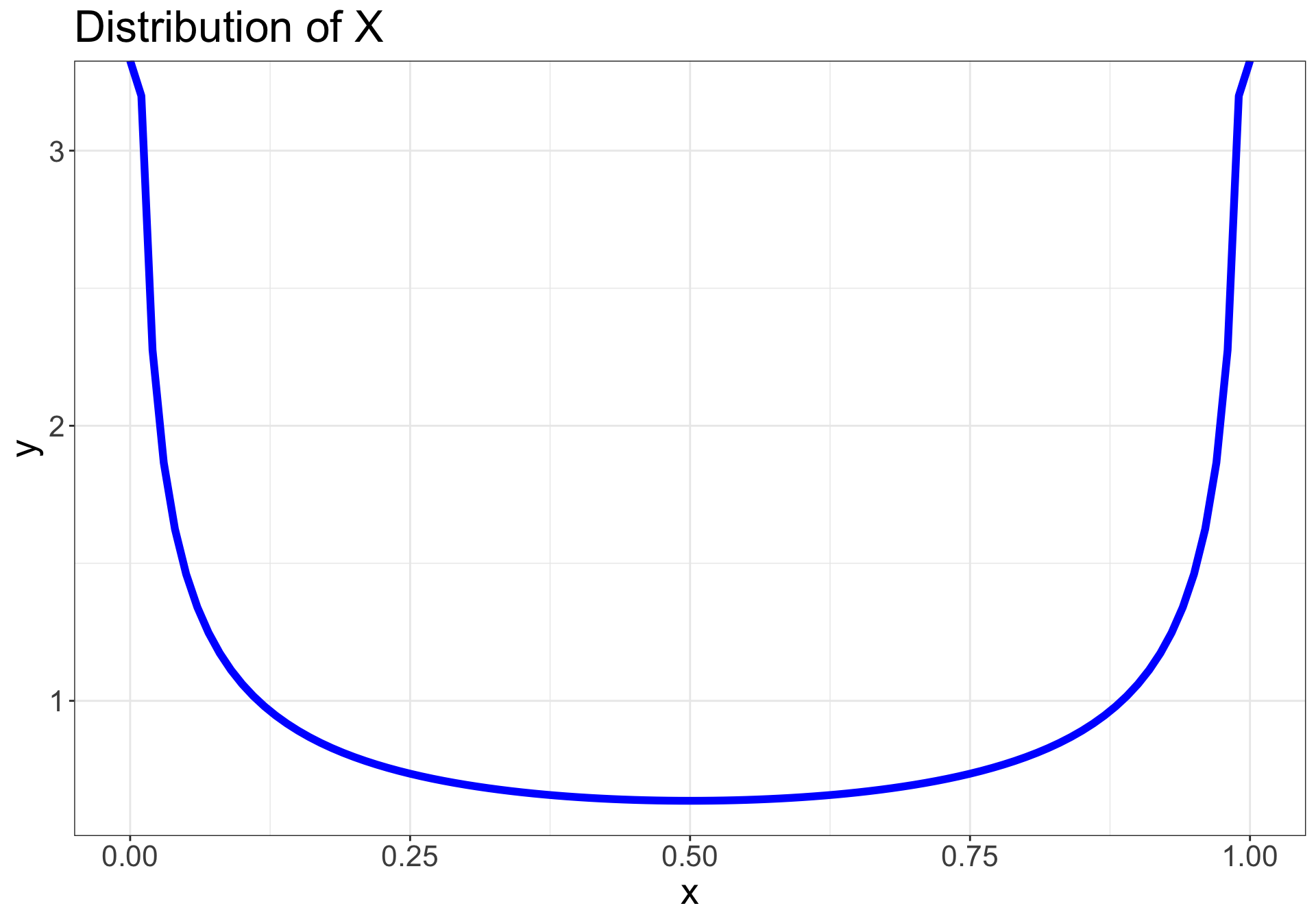
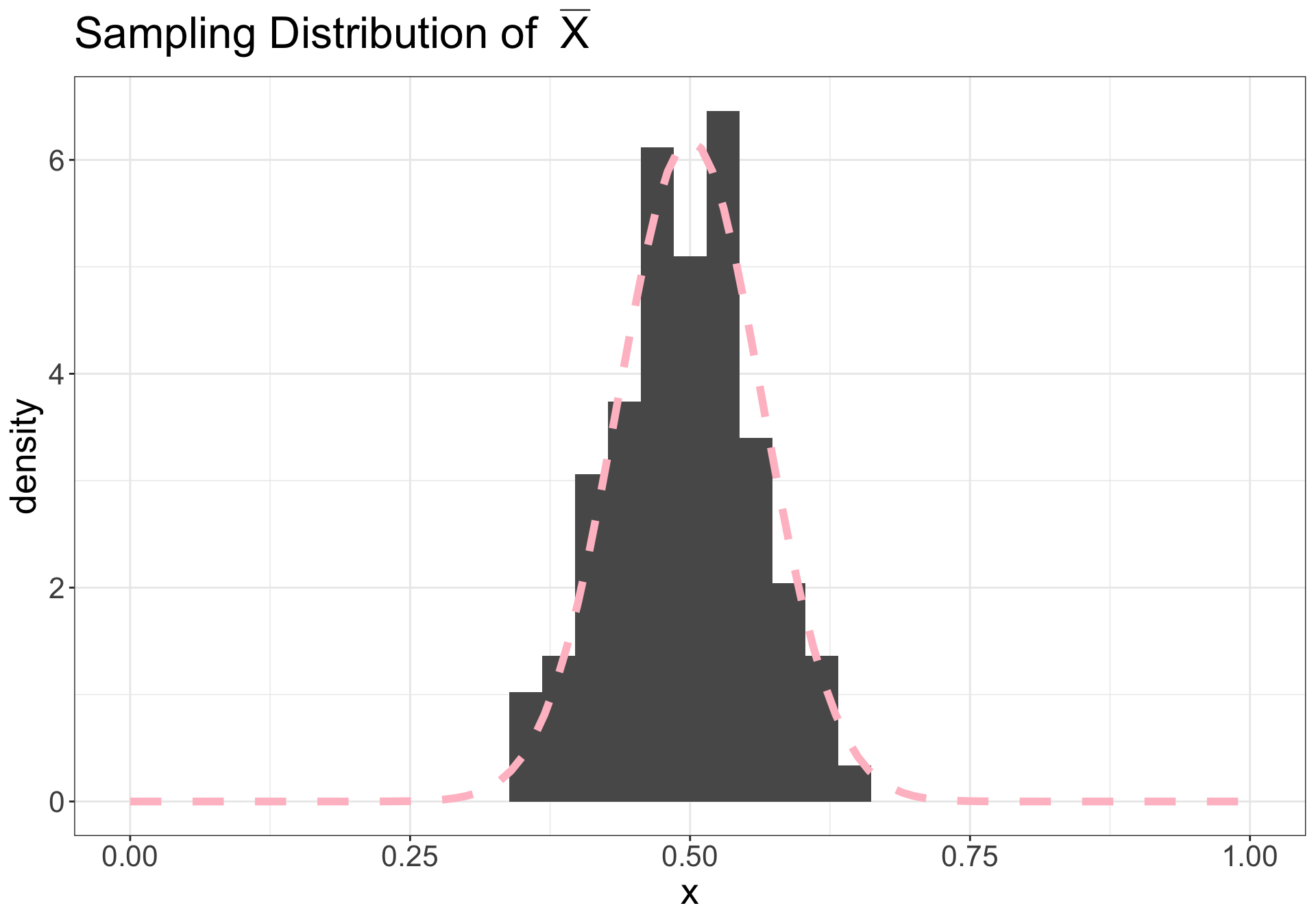
On right: dashed pink line is \(N(\mu, \sigma^2/n)\)
Illustration (n = 100)
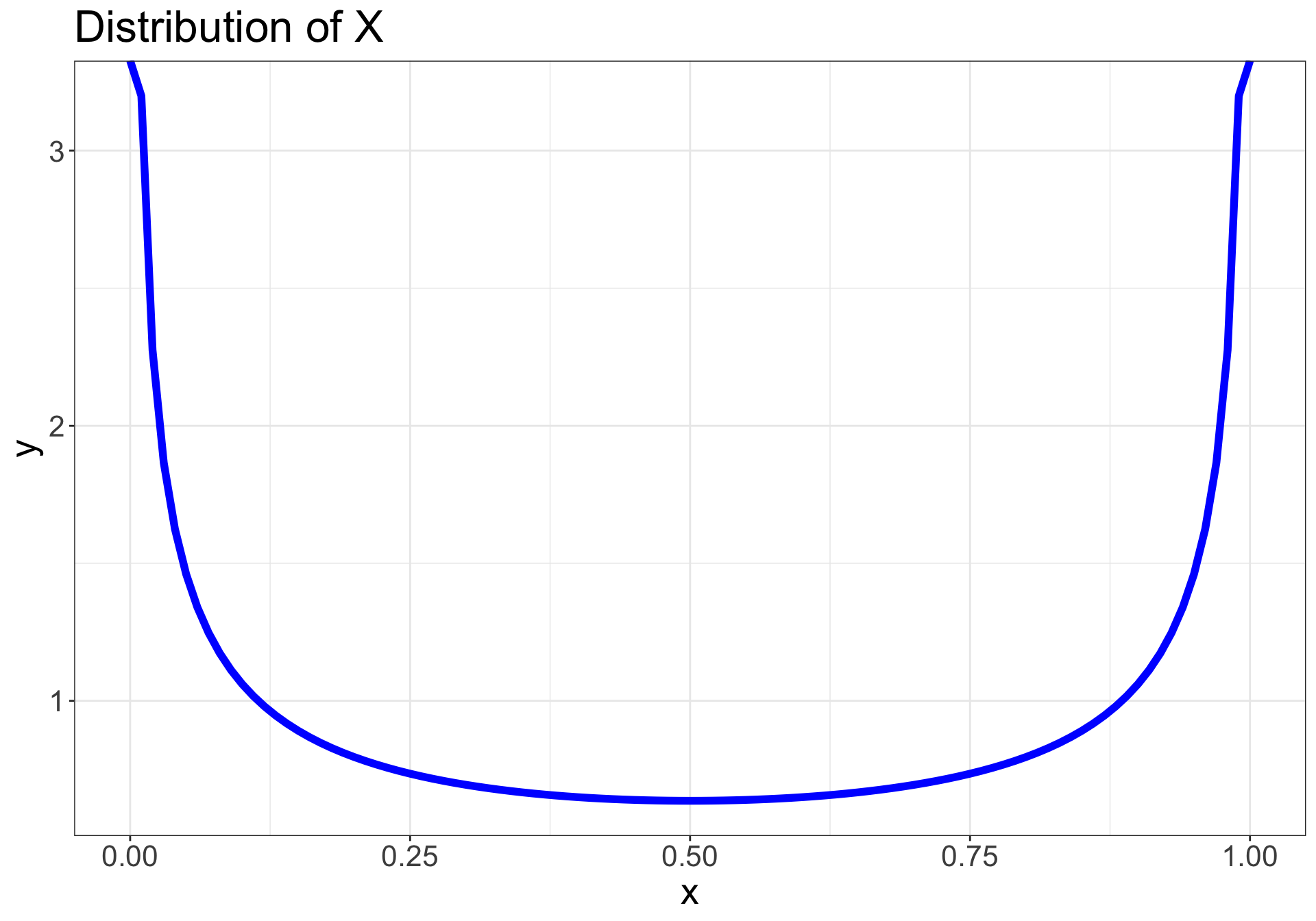
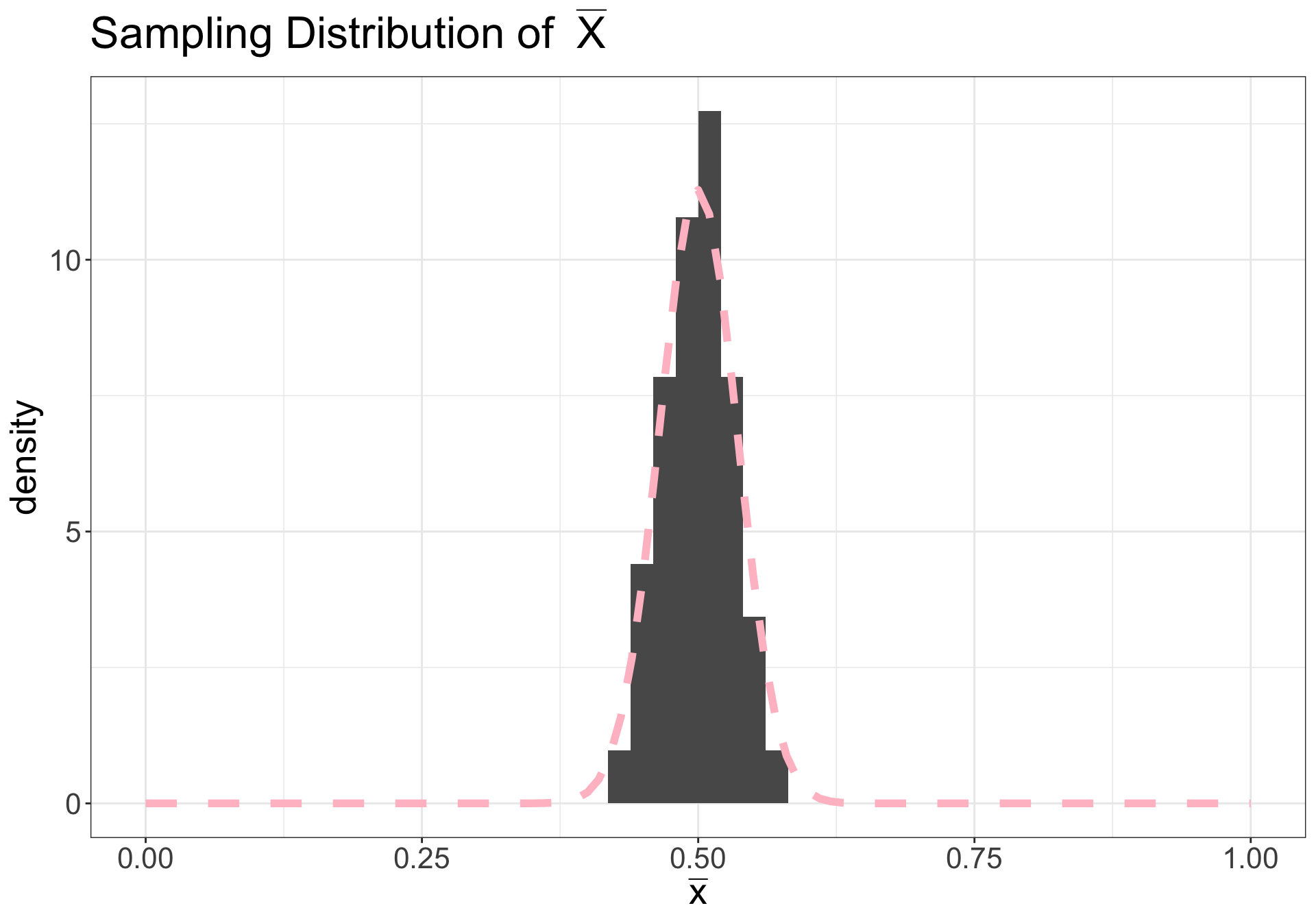
On right: dashed pink line is \(N(\mu, \sigma^2/n)\)
Hypothesis Testing
Hypothesis: A testable (falsifiable) idea for explaining a phenomenon
Statistical hypothesis: A hypothesis that is testable on the basis of observing a process that is modeled via a set of random variables
Hypothesis Testing: A formal procedure for determining whether to accept or reject a statistical hypothesis
Requires comparing two hypotheses:
\(H_0\): null hypothesis
\(H_A\) or \(H_1\): alternative hypothesis
Hypothesis Testing: Motivating Example
- The expression level of gene \(\normalsize g\) is measured in \(\normalsize n\) patients with disease (e.g. cancer), and \(\normalsize m\) healthy (control) individuals:
- \(\normalsize z_1, z_2, ..., z_n\) and \(\normalsize y_1, y_2, ..., y_m\)
- Is gene \(\normalsize g\) differentially expressed in cancer vs healthy samples?
- \(\normalsize H_0: \mu_Z = \mu_Y\)
- \(\normalsize H_A: \mu_Z \neq \mu_Y\)
- In this setting, hypothesis testing allows us to determine whether observed differences between groups in our data are significant
Steps in Hypothesis Testing
Formulate your hypothesis as a statistical hypothesis
Define a test statistic \(t\) (RV) that corresponds to the question. You need to know the expected distribution of the test statistic under the null
Compute the p-value associated with the observed test statistic under the null distribution \(\normalsize p(t | H_0)\)
Motivating example (cancer vs healthy gene expression)
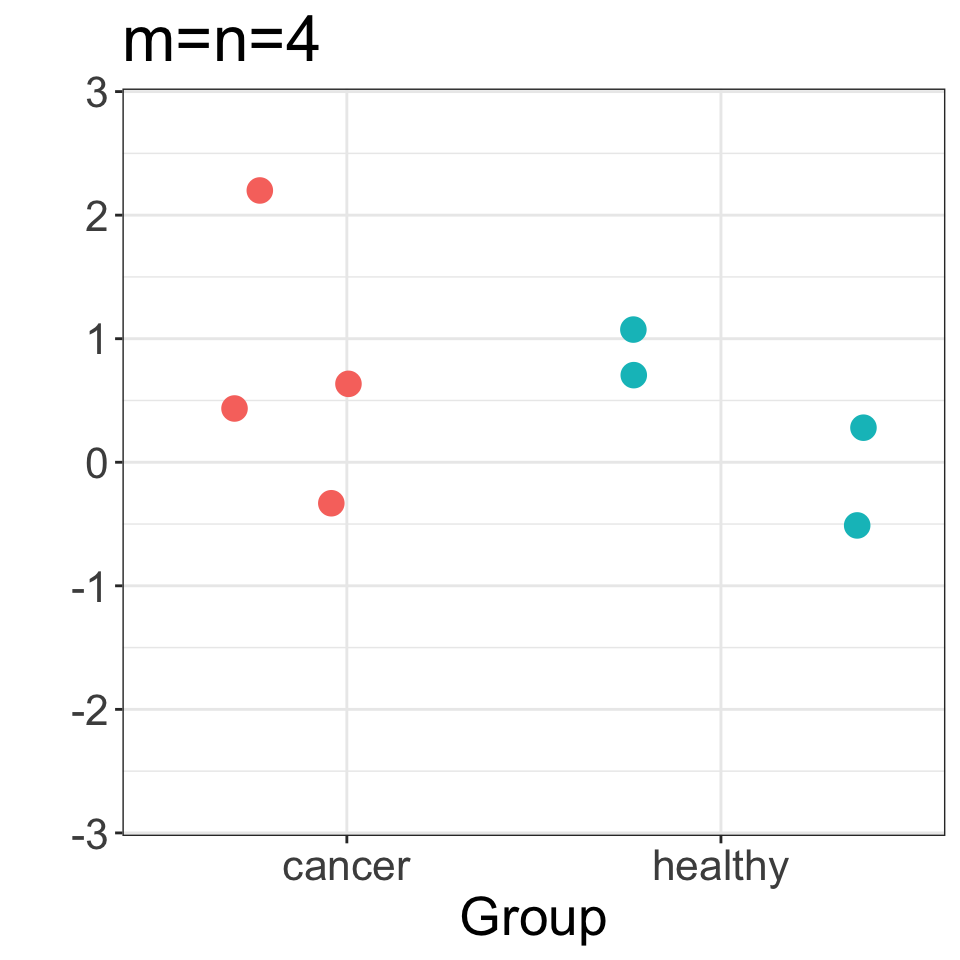
Motivating example (cancer vs healthy gene expression)
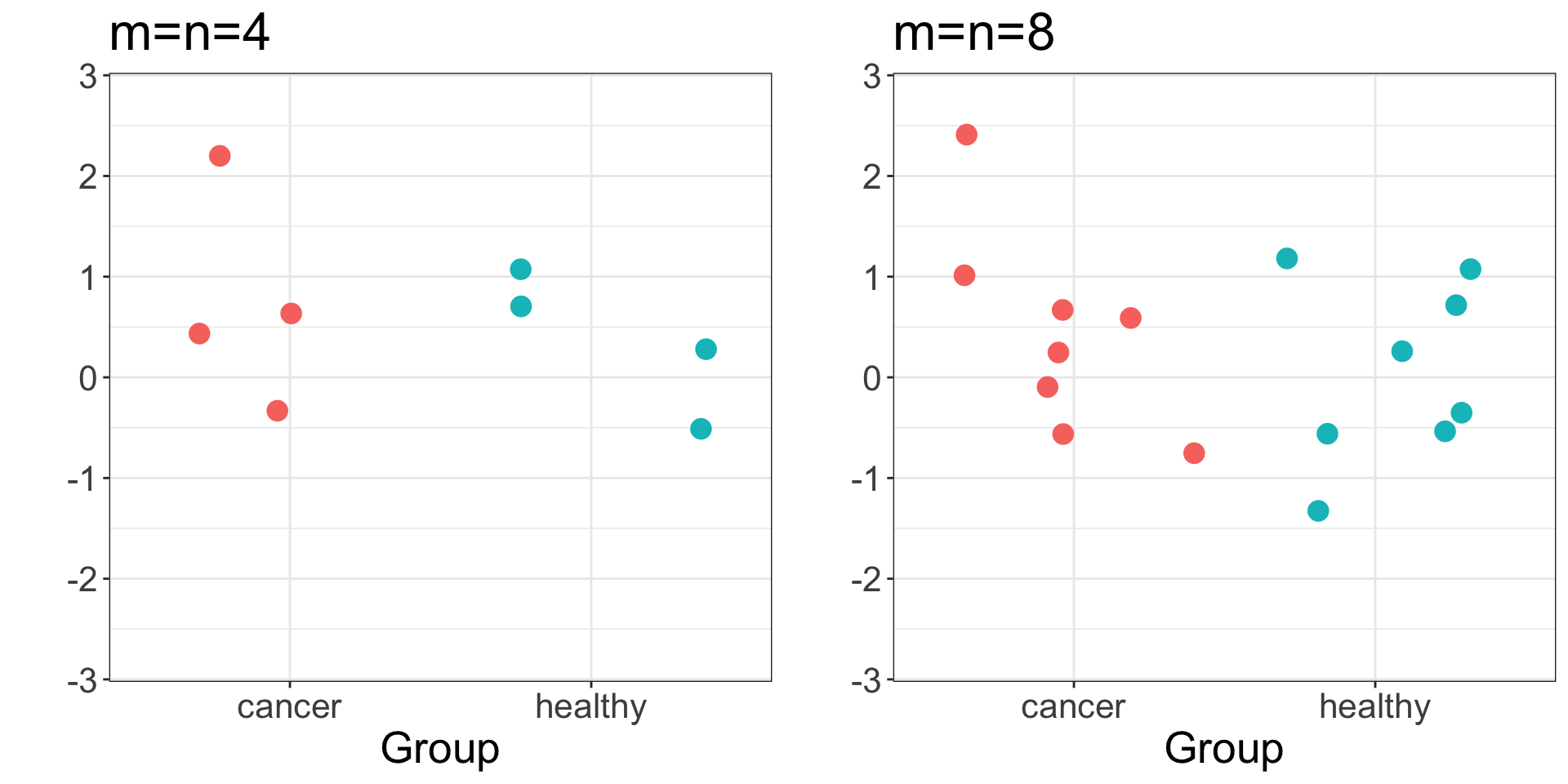
Motivating example (cancer vs healthy gene expression)
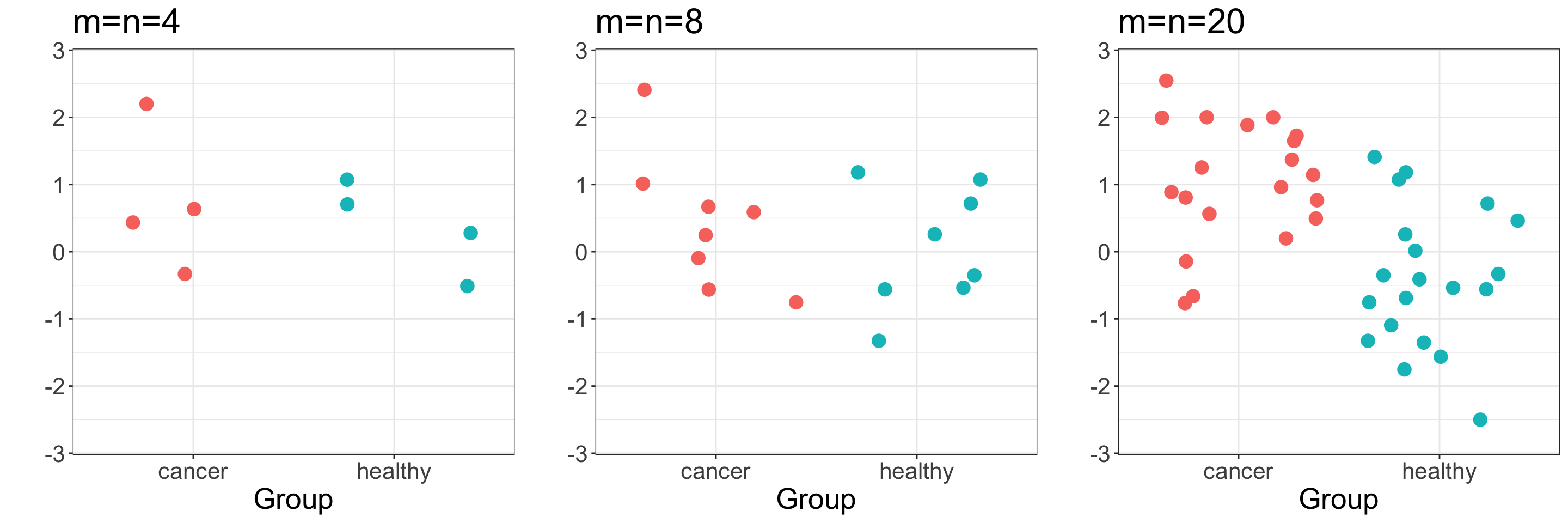
- Is there a significant difference between the two means?
- Samples drawn from independent Normal distributions with equal variance and \(\mu_Z-\mu_Y=1\)
Is there a significant difference between the two means?
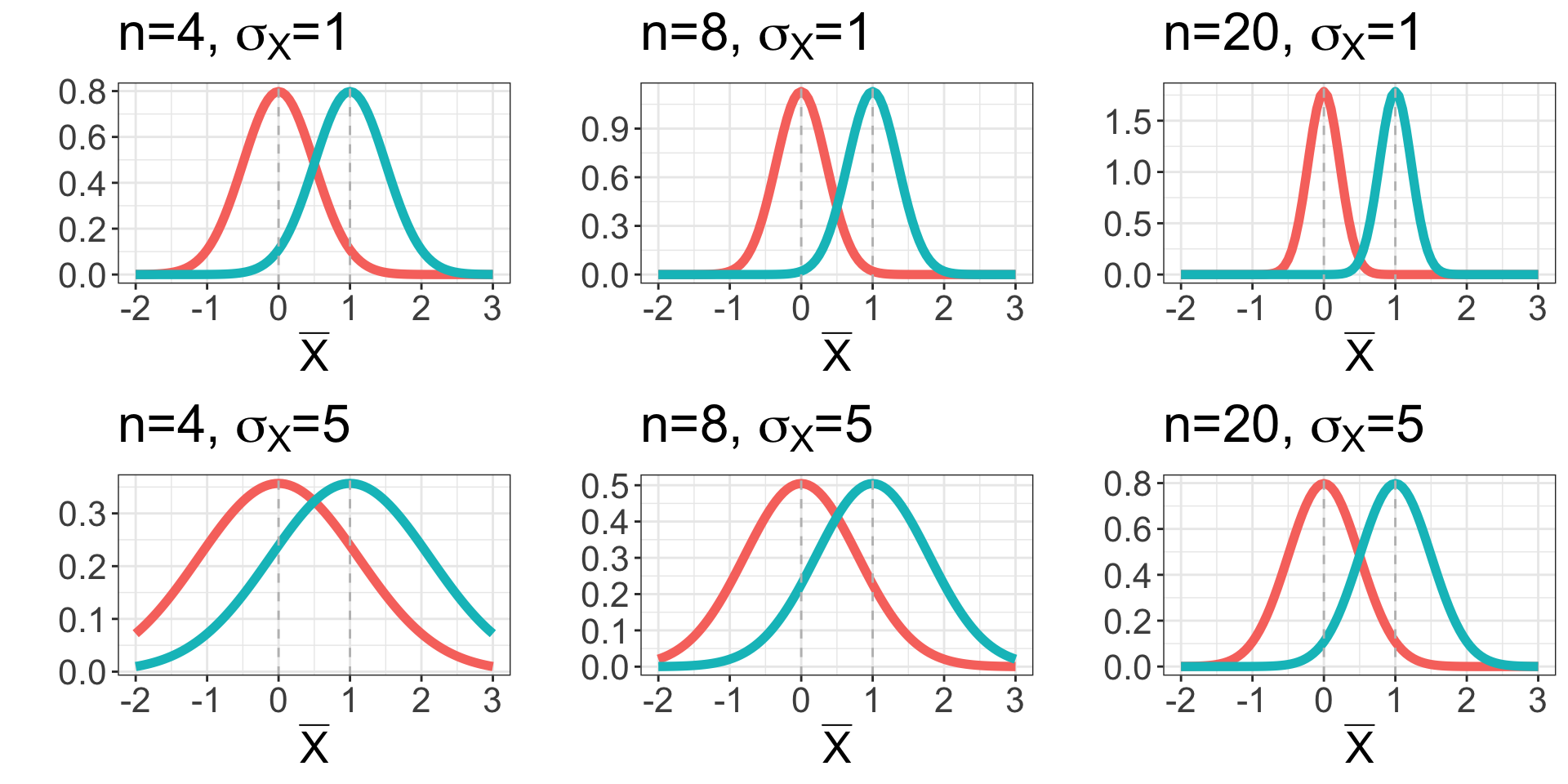
Which panel looks most significant?
Which looks least significant?
Is there a significant difference between the two means?

Mean difference needs to be put into context of the __________________ and __________________. Recall the formula for the sampling distribution of the mean:
2 sample t-statistic
- 2-sample t-statistic: measures difference in means, adjusted for spread/standard deviation:
\[\normalsize t=\frac{\bar{z}-\bar{y}}{SE_{\bar{z}-\bar{y}}}\] e.g. for \(z_1, z_2, ..., z_n\) expression measurements in healthy samples and \(y_1, y_2, ..., y_m\) cancer samples
- From the theory, we know the distribution of our test statistic, if we are willing to make some assumptions
2 sample t-test
If we assume:
\(\bar{Z}\) and \(\bar{Y}\) are normally distributed
\(Z\) and \(Y\) have equal variance
Then the standard error estimate for the difference in means is:
\[SE_{\bar{z}-\bar{y}} = s_p \sqrt{\frac{1}{n} + \frac{1}{m}} \text{ , where } s_p^2 = \frac{(n-1)s^2_z + (m-1)s^2_y}{(n-1) + (m-1)}\]
And our t-statistic follows a t distribution with m+n-2 degrees of freedom \[t \sim t_{n+m-2}\]
(Alternative formulations for unequal variance setting)
t distribution

statistic value tells us how extreme our observed data is relative to the null
obtain p-value by computing area to the left and/or right of the t statistic (one-sided vs two-sided)
Summary
Random variables are variables that have a probability distribution
Any statistic of sampled data is a RV, and hence has an associated probability distribution
The CLT gives us the sampling distribution of the mean of any RV (regardless of its distribution)
We can use statistical inference to estimate population parameters from a sample
Hypothesis testing gives us a framework to assess a statistical hypothesis